from numpy.linalg import cholesky, det
from scipy.linalg import solve_triangular
from scipy.optimize import minimize
from matplotlib import pyplot as plt
def nll_fn(X_train, Y_train, noise, naive=True):
"""
Returns a function that computes the negative log marginal
likelihood for training data X_train and Y_train and given
noise level.
Args:
X_train: training locations (m x d).
Y_train: training targets (m x 1).
noise: known noise level of Y_train.
naive: if True use a naive implementation of Eq. (11), if
False use a numerically more stable implementation.
Returns:
Minimization objective.
"""
Y_train = Y_train.ravel()
def nll_naive(theta):
# Naive implementation of Eq. (11). Works well for the examples
# in this article but is numerically less stable compared to
# the implementation in nll_stable below.
K = kernel(X_train, X_train, l=theta[0], sigma=theta[1]) + \
noise**2 * np.eye(len(X_train))
return 0.5 * np.log(det(K)) + \
0.5 * Y_train.dot(inv(K).dot(Y_train)) + \
0.5 * len(X_train) * np.log(2*np.pi)
def nll_stable(theta):
# Numerically more stable implementation of Eq. (11) as described
# in http://www.gaussianprocess.org/gpml/chapters/RW2.pdf, Section
# 2.2, Algorithm 2.1.
K = kernel(X_train, X_train, l=theta[0], sigma=theta[1]) + \
noise**2 * np.eye(len(X_train))
L = cholesky(K)
S1 = solve_triangular(L, Y_train, lower=True)
S2 = solve_triangular(L.T, S1, lower=False)
return np.sum(np.log(np.diagonal(L))) + \
0.5 * Y_train.dot(S2) + \
0.5 * len(X_train) * np.log(2*np.pi)
if naive:
return nll_naive
else:
return nll_stable
from helper import plot_gp_2D
noise_2D = 0.1
rx, ry = np.arange(-5, 5, 0.3), np.arange(-5, 5, 0.3)
gx, gy = np.meshgrid(rx, rx)
X_2D = np.c_[gx.ravel(), gy.ravel()]
X_2D_train = np.random.uniform(-4, 4, (100, 2))
Y_2D_train = np.sin(0.5 * np.linalg.norm(X_2D_train, axis=1)) + \
noise_2D * np.random.randn(len(X_2D_train))
plt.figure(figsize=(14,7))
mu_s, _ = posterior(X_2D, X_2D_train, Y_2D_train, sigma_y=noise_2D)
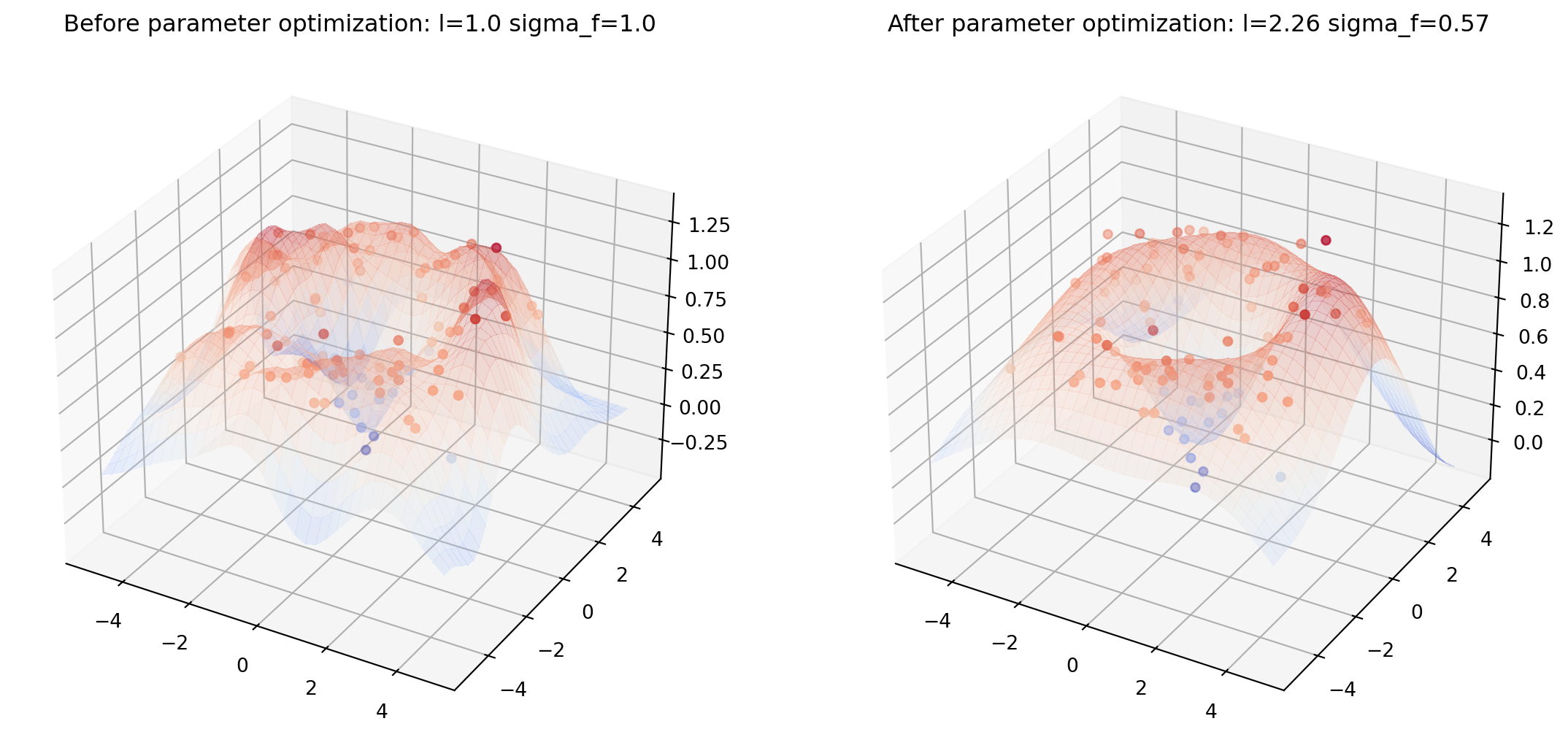
plot_gp_2D(gx, gy, mu_s, X_2D_train, Y_2D_train,
f'Before parameter optimization: l={1.00} sigma_f={1.00}', 1)
res = minimize(nll_fn(X_2D_train, Y_2D_train, noise_2D), [1, 1],
bounds=((1e-5, None), (1e-5, None)),
method='L-BFGS-B')
mu_s, _ = posterior(X_2D, X_2D_train, Y_2D_train, *res.x, sigma_y=noise_2D)
plot_gp_2D(gx, gy, mu_s, X_2D_train, Y_2D_train,
f'After parameter optimization: l={res.x[0]:.2f} sigma_f={res.x[1]:.2f}', 2)