Automatizace ve fyzice: Bayesovská optimalizace

Author

Petr Čermák

Published

November 28, 2024

Připojte se

cermak.science/teaching/automation/lectures/08-bo/

Statistika v kostce

Obecné pojmy - pravděpodobnostní model

Likehood funkce

funkce věrohodnosti
$\mathcal{L}(\theta; D)$
vyjadřuje pravděpodobnost, že by daná sada parametrů $\theta$ generovala pozorovaná data $D$.

Náhodný proces

výsledkem je funkce

Modely

parametrické (konečný/malý počet parametrů)
non-parametric (nekonečně/hodně) parametrů (třeba SG filter)

non-parametric: Savitzky–Golay filter (lokální aproximace polynomy)

Obecné pojmy

Metoda maximální věrohodnosti

MLE (Maximum likelihood estimation)
hledám parametry modelu, které vygenerují naměřená data s největší pravděpodobností

Maximální aposteriorní odhad

MAP (Maximum a Posteriori Estimation)
Parametry nejsou náhodné, známe jejich distribuci
Kombinace likehood funkce a apriorní informace o parametrech

\[ \hat{\theta}_{\text{MLE}} = \arg \max_{\theta} \mathcal{L}(\theta; D) \]

\[ P(\theta | D) = \frac{P(D | \theta) \cdot P(\theta)}{P(D)} \]

\[ \hat{\theta}_{\text{MAP}} = \arg \max_{\theta} P(\theta | D) \]

Gaussovské procesy

Gaussovský proces

model náhodného procesu
neparametrický
hodnoty jsou náhodné proměné, vzájemně korelované
popisuje ho střední hodnota a kovarianční funkce (určuje hladkost)
pro dva blízké body $x_j$ a $x_i$ platí, že jejich $f(x_n$)$ jsou také blízké
za pomoci tréninkového datasetu umí predikovat další hodnoty

Příklad jádra (kovarianční fce): RBF

RBF (Radial Basis Function, jádro exponentu kvadratického) \[ \kappa(\mathbf{x}_i,\mathbf{x}_j) = \sigma^2 \exp\left(-\frac{\|\mathbf{x}_i - \mathbf{x}_j\|^2}{2l^2}\right) \]

kde $l$ ovlivňuje jak rychle korelace klesá a $\sigma$ určuje škálování jádra.

import numpy as np

def kernel(X1, X2, l=1.0, sigma=1.0):
    """
    Isotropic squared exponential kernel.
    
    Args:
        X1,2: Array of m points (m x d).
        X2: Array of n points (n x d).

    Returns:
        (m x n) matrix.
    """
    sqdist = np.sum(X1**2, 1).reshape(-1, 1) + np.sum(X2**2, 1) - 2 * np.dot(X1, X2.T)
    return sigma**2 * np.exp(-0.5 / l**2 * sqdist)

Prior (nevíme nic)

from helper import plot_gp

# Vygeneruji body (konečný počet)
X = np.arange(0, 10, 0.1).reshape(-1, 1) #počet sloupců dopočítá

mu = np.zeros(X.shape)   # střední hodnota
cov = kernel(X, X)       # spočtu kovarianci (nenormovaná korelace)

# Vygeneruji 5 funkcí jako výsledek náhodného gaussovského procesu
samples = np.random.multivariate_normal(mu.ravel(), cov, 5)

# Vykreslí střední hodnotu, oblast nejistoty a funkce 
plot_gp(mu, cov, X, samples=samples)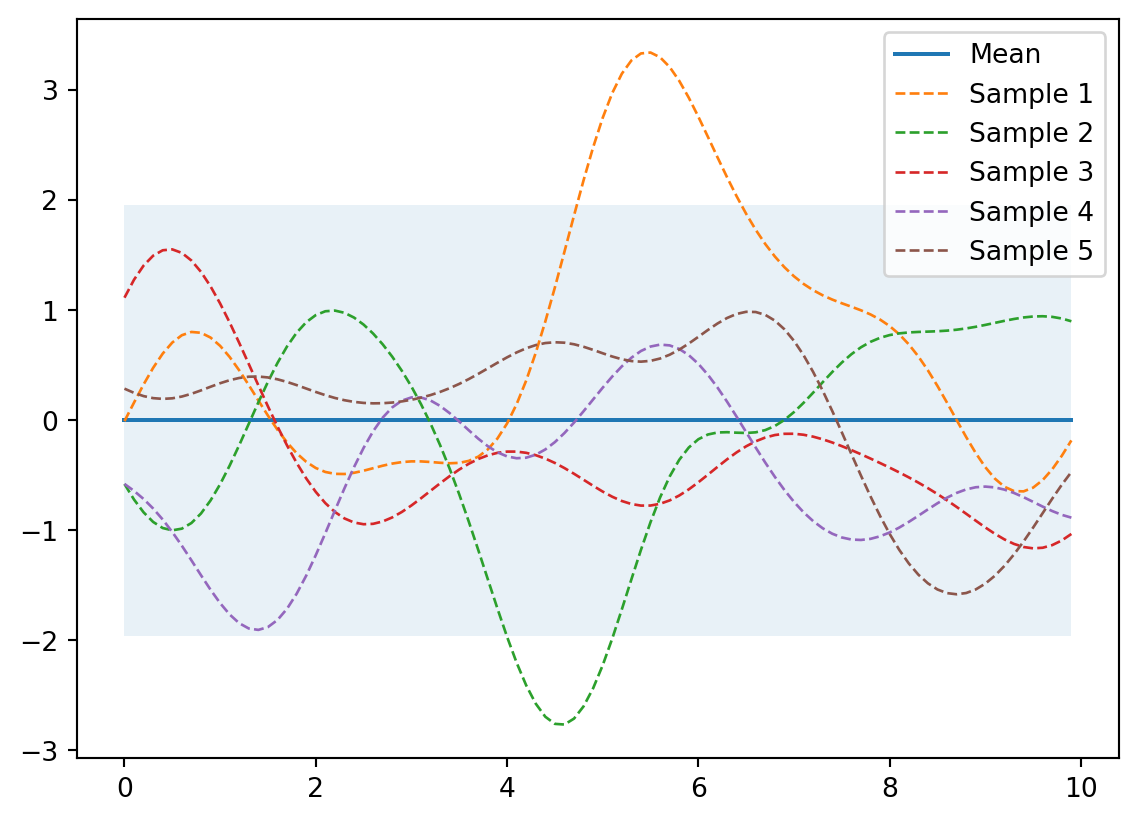

Posterior

from numpy.linalg import inv

def posterior(X, X_train, Y_train, l=1.0, sigma=1.0, sigma_y=1e-8):
    """
    Spočítá novou střední hodnotu a kovarianci při znalosti train dat
    
    Args:
        X: osa x
        X_train, Y_train: známá data (m x 1)
        l, sigma: Parametry jádra
        sigma_y: šum
    
    Returns:
        Posterior střední hodnota (n x d) a kovariance (n x n).
    """
    K = kernel(X_train, X_train, l, sigma) + sigma_y**2 * np.eye(len(X_train))  
    # jádro s šumem
    K_s = kernel(X_train, X, l, sigma)
    K_ss = kernel(X, X, l, sigma) + 1e-8 * np.eye(len(X))
    
    mu_s = K_s.T.dot(inv(K)).dot(Y_train)     # (7)
    
    cov_s = K_ss - K_s.T.dot(inv(K)).dot(K_s) # (8)
    return mu_s, cov_s

\[ \begin{equation} \mathbf{\mu_*} = \mathbf{K}_*^T \mathbf{K}_y^{-1} \mathbf{y} \tag{7} % Nastavení vlastního číslování \end{equation} \] \[ \begin{equation} \mathbf{\Sigma_*} = \mathbf{K}_{**} - \mathbf{K}_*^T \mathbf{K}_y^{-1} \mathbf{K}_* \tag{8} % Nastavení vlastního číslování \end{equation} \]

Odvození zde.

Zadáme data (bez šumu)

# Zadáme data
X_train = np.array([1, 3, 4]).reshape(-1, 1)
Y_train = np.sin(X_train)
# Spočteme novou (posterior) střední hodnotu a kovarianci
mu_s, cov_s = posterior(X, X_train, Y_train)
samples = np.random.multivariate_normal(mu_s.ravel(), cov_s, 3)
plot_gp(mu_s, cov_s, X, X_train=X_train, Y_train=Y_train, samples=samples)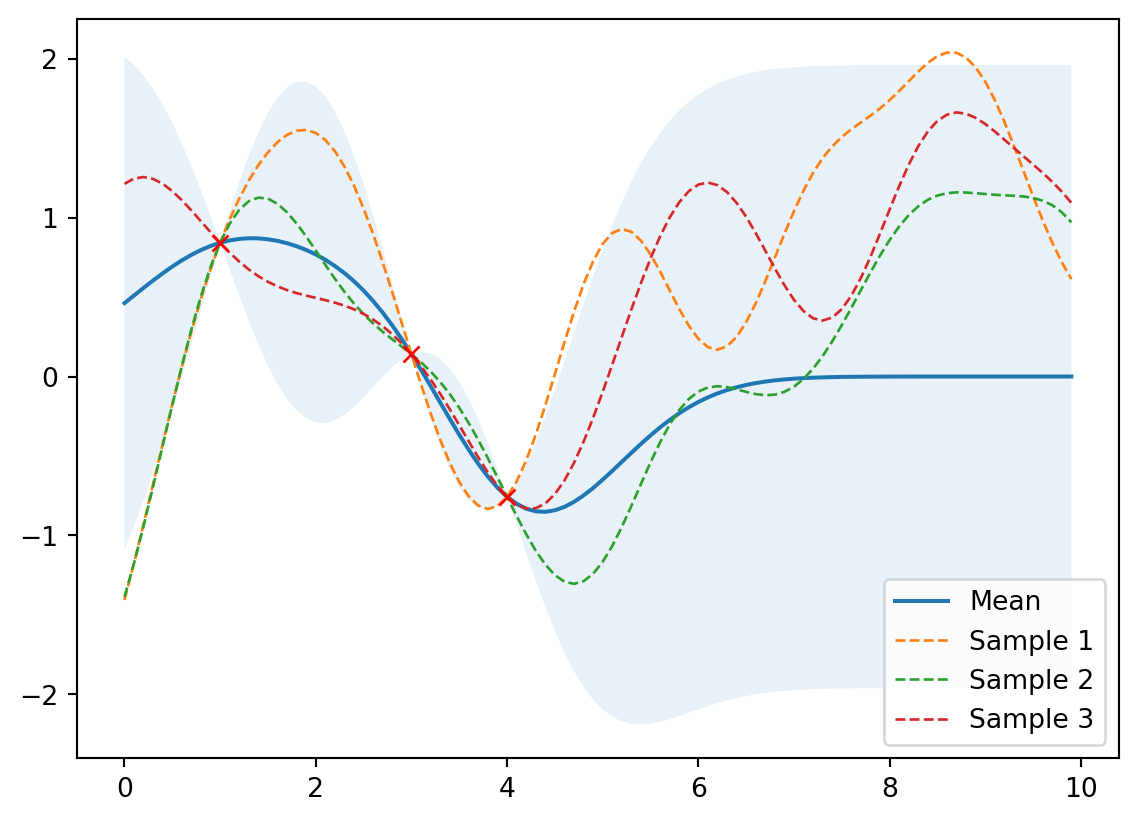

To není dokonalé - ta data nejsou z principu přesná.

Zadáme data (se šumem)

# Zašuměná data
noise = 0.2
X_train = np.arange(0, 5, 1).reshape(-1, 1)
Y_train = np.sin(X_train) + noise * np.random.randn(*X_train.shape)
mu_s, cov_s = posterior(X, X_train, Y_train, sigma_y=noise)
samples = np.random.multivariate_normal(mu_s.ravel(), cov_s, 3)
plot_gp(mu_s, cov_s, X, X_train=X_train, Y_train=Y_train, samples=samples)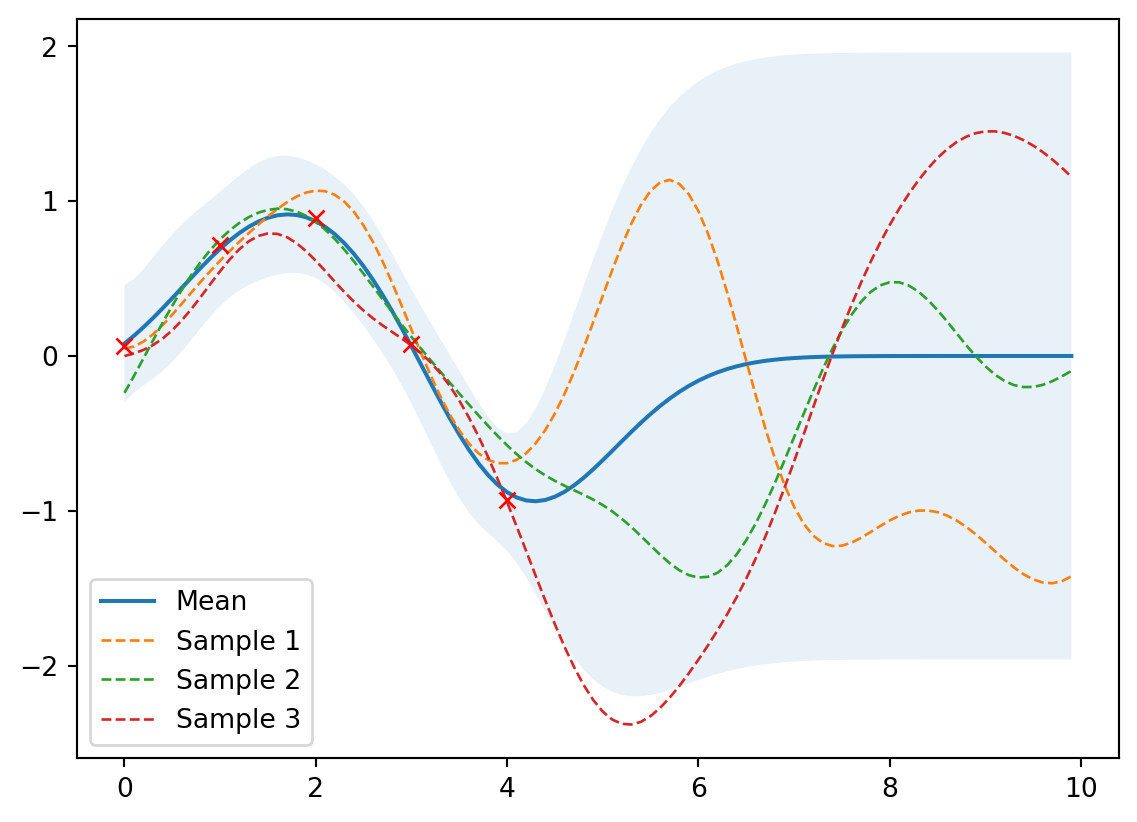

Fajn, jak nastavit ty parametry?

Vliv parametrů

Ukaž kód

import matplotlib.pyplot as plt

params = [
    (0.3, 1.0, 0.2),
    (3.0, 1.0, 0.2),
    (1.0, 0.3, 0.2),
    (1.0, 3.0, 0.2),
    (1.0, 1.0, 0.05),
    (1.0, 1.0, 1.5),
]

plt.figure(figsize=(13, 2.5))

for i, (l, sigma, sigma_y) in enumerate(params):
    mu_s, cov_s = posterior(X, X_train, Y_train, l=l, 
                            sigma=sigma, 
                            sigma_y=sigma_y)
    plt.subplot(2, 3, i + 1)
    plt.subplots_adjust(top=2)
    plt.title(f'l = {l}, sigma = {sigma}, sigma_y = {sigma_y}')
    plot_gp(mu_s, cov_s, X, X_train=X_train, Y_train=Y_train)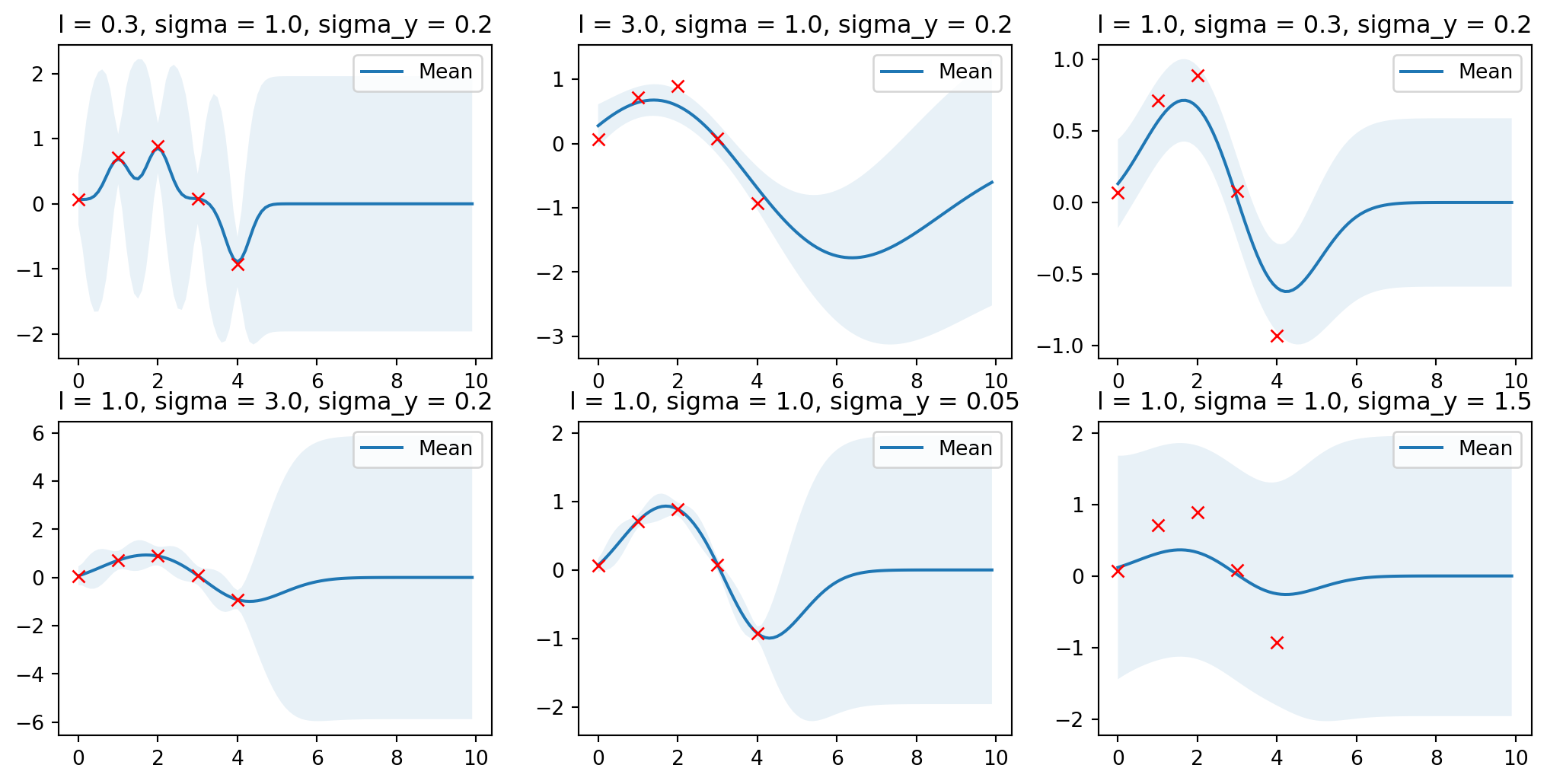

Optimální parametry

Lze nalézt optimální parametry

\[ \log p(\mathbf{y} \lvert \mathbf{X}) = \log \mathcal{N}(\mathbf{y} \lvert \mathbf{0},\mathbf{K}_y) = -\frac{1}{2} \mathbf{y}^T \mathbf{K}_y^{-1} \mathbf{y} -\frac{1}{2} \log \begin{vmatrix}\mathbf{K}_y\end{vmatrix} -\frac{N}{2} \log(2\pi) \]

Kód zde

from numpy.linalg import cholesky, det
from scipy.linalg import solve_triangular
from scipy.optimize import minimize

def nll_fn(X_train, Y_train, noise, naive=True):
    """
    Returns a function that computes the negative log marginal
    likelihood for training data X_train and Y_train and given
    noise level.

    Args:
        X_train: training locations (m x d).
        Y_train: training targets (m x 1).
        noise: known noise level of Y_train.
        naive: if True use a naive implementation of Eq. (11), if
               False use a numerically more stable implementation.

    Returns:
        Minimization objective.
    """
    
    Y_train = Y_train.ravel()
    
    def nll_naive(theta):
        # Naive implementation of Eq. (11). Works well for the examples 
        # in this article but is numerically less stable compared to 
        # the implementation in nll_stable below.
        K = kernel(X_train, X_train, l=theta[0], sigma=theta[1]) + \
            noise**2 * np.eye(len(X_train))
        return 0.5 * np.log(det(K)) + \
               0.5 * Y_train.dot(inv(K).dot(Y_train)) + \
               0.5 * len(X_train) * np.log(2*np.pi)
        
    def nll_stable(theta):
        # Numerically more stable implementation of Eq. (11) as described
        # in http://www.gaussianprocess.org/gpml/chapters/RW2.pdf, Section
        # 2.2, Algorithm 2.1.
        
        K = kernel(X_train, X_train, l=theta[0], sigma=theta[1]) + \
            noise**2 * np.eye(len(X_train))
        L = cholesky(K)
        
        S1 = solve_triangular(L, Y_train, lower=True)
        S2 = solve_triangular(L.T, S1, lower=False)
        
        return np.sum(np.log(np.diagonal(L))) + \
               0.5 * Y_train.dot(S2) + \
               0.5 * len(X_train) * np.log(2*np.pi)

    if naive:
        return nll_naive
    else:
        return nll_stable

# Minimize the negative log-likelihood w.r.t. parameters l and sigma_f.
# We should actually run the minimization several times with different
# initializations to avoid local minima but this is skipped here for
# simplicity.
res = minimize(nll_fn(X_train, Y_train, noise), [1, 1], 
               bounds=((1e-5, None), (1e-5, None)),
               method='L-BFGS-B')

# Store the optimization results in global variables so that we can
# compare it later with the results from other implementations.
l_opt, sigma_f_opt = res.x

# Compute posterior mean and covariance with optimized kernel parameters and plot the results
mu_s, cov_s = posterior(X, X_train, Y_train, l=l_opt, sigma=sigma_f_opt, sigma_y=noise)
plt.figure(figsize=(13, 4))
plot_gp(mu_s, cov_s, X, X_train=X_train, Y_train=Y_train)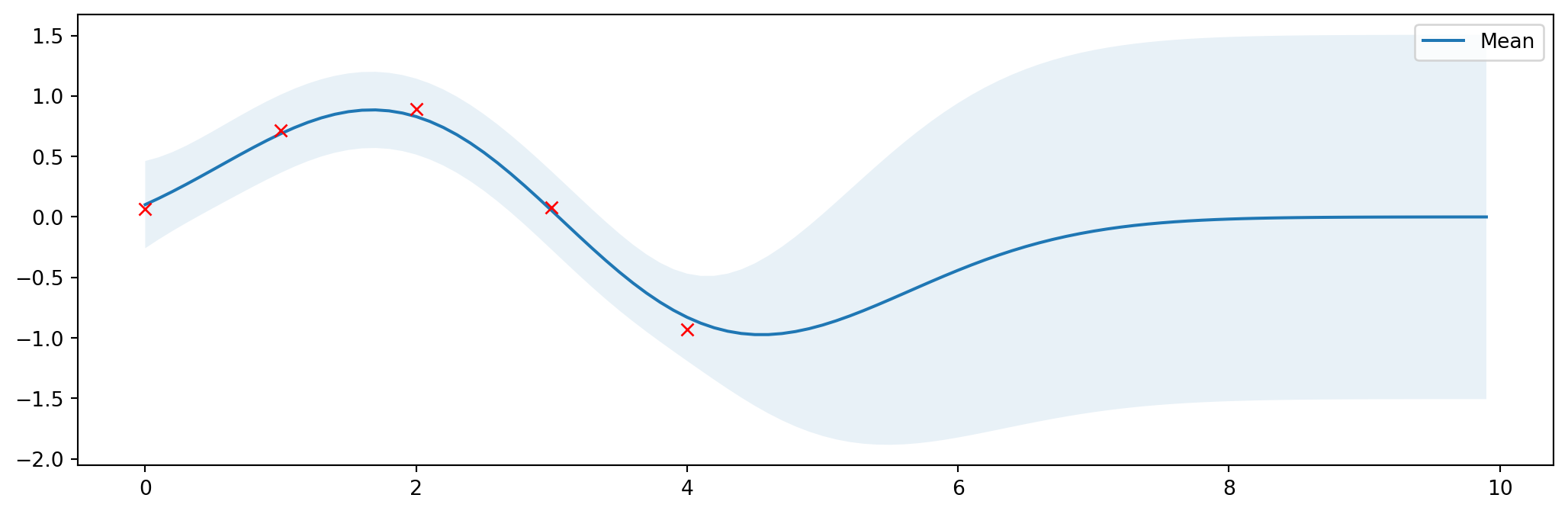

Více rozměrů

Kód zde

from helper import plot_gp_2D

noise_2D = 0.1

rx, ry = np.arange(-5, 5, 0.3), np.arange(-5, 5, 0.3)
gx, gy = np.meshgrid(rx, rx)

X_2D = np.c_[gx.ravel(), gy.ravel()]

X_2D_train = np.random.uniform(-4, 4, (100, 2))
Y_2D_train = np.sin(0.5 * np.linalg.norm(X_2D_train, axis=1)) + \
             noise_2D * np.random.randn(len(X_2D_train))

plt.figure(figsize=(14,7))

mu_s, _ = posterior(X_2D, X_2D_train, Y_2D_train, sigma_y=noise_2D)
plot_gp_2D(gx, gy, mu_s, X_2D_train, Y_2D_train, 
           f'Before parameter optimization: l={1.00} sigma_f={1.00}', 1)

res = minimize(nll_fn(X_2D_train, Y_2D_train, noise_2D), [1, 1], 
               bounds=((1e-5, None), (1e-5, None)),
               method='L-BFGS-B')

mu_s, _ = posterior(X_2D, X_2D_train, Y_2D_train, *res.x, sigma_y=noise_2D)
plot_gp_2D(gx, gy, mu_s, X_2D_train, Y_2D_train,
           f'After parameter optimization: l={res.x[0]:.2f} sigma_f={res.x[1]:.2f}', 2)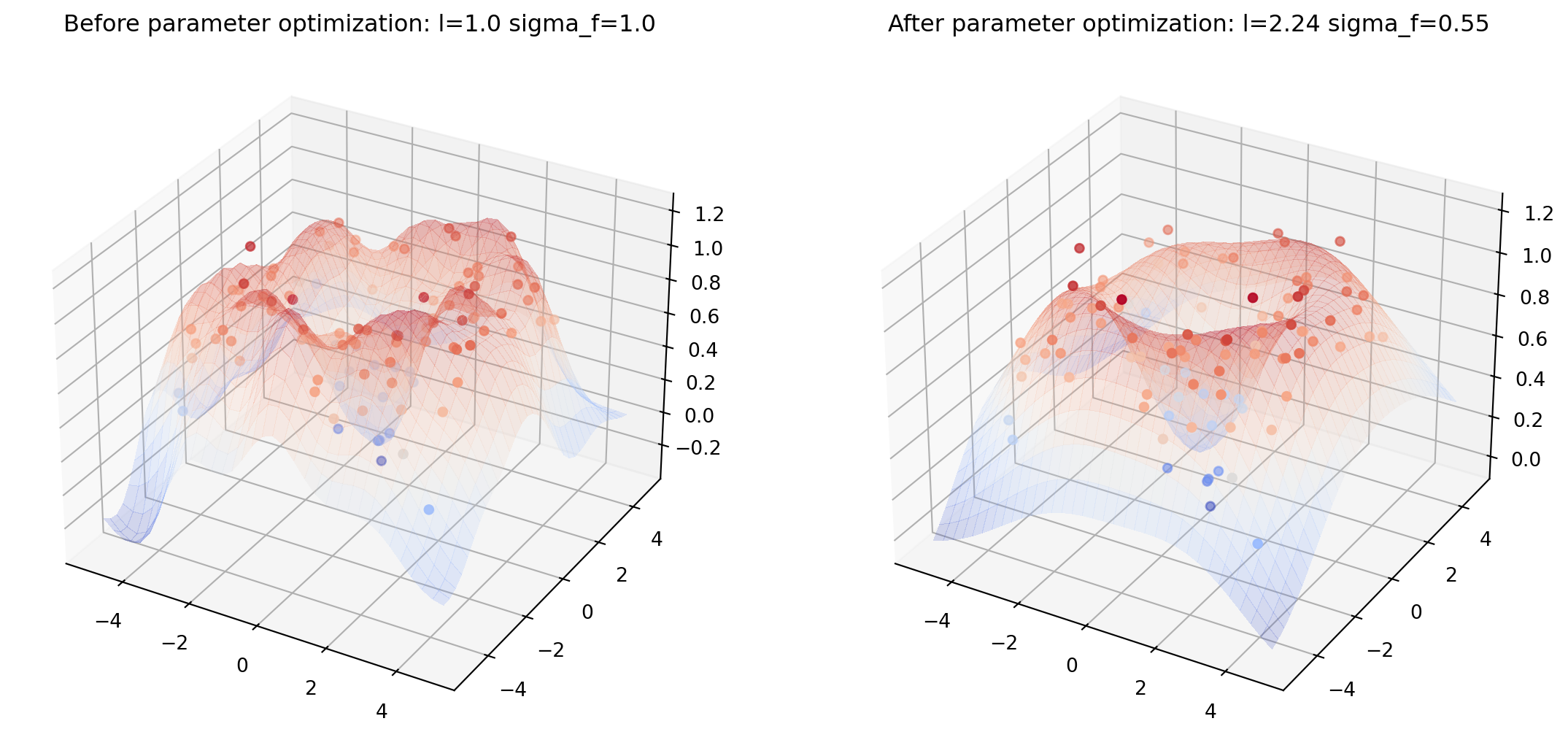

Jsou na to knihovny

Scikit-learn

GaussianProcessRegressor vytváří posterior data (“fituje hodnoty”)
Připravená jádra

from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn.gaussian_process.kernels import ConstantKernel, RBF

rbf = ConstantKernel(1.0) * RBF(length_scale=1.0)
gpr = GaussianProcessRegressor(kernel=rbf, alpha=noise**2)

# Použiju stará data
gpr.fit(X_train, Y_train)

# Výpočet posterior parametrů
mu_s, cov_s = gpr.predict(X, return_cov=True)

# Optimalizované parametry Gausse
l = gpr.kernel_.k2.get_params()['length_scale']
sigma = np.sqrt(gpr.kernel_.k1.get_params()['constant_value'])

plot_gp(mu_s, cov_s, X, X_train=X_train, Y_train=Y_train)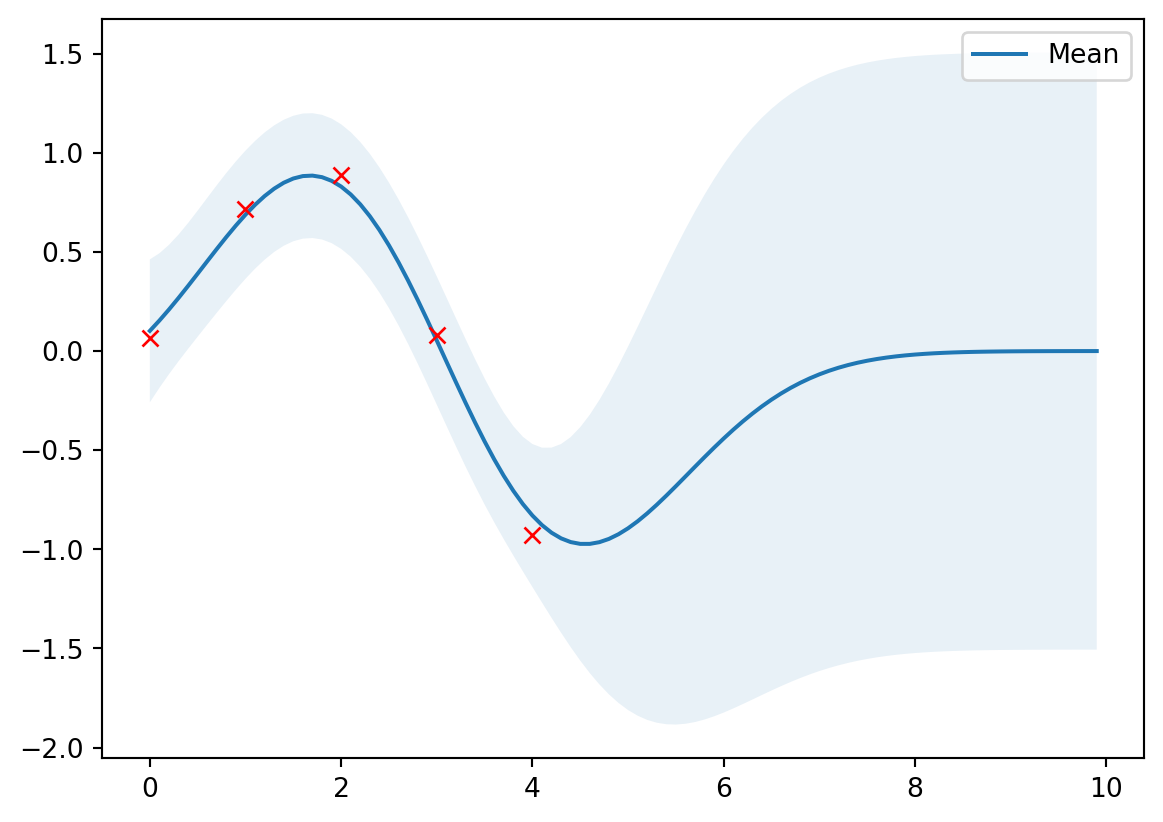

Knihovna GPy

Vyvíjeno Sheffield machine learning group.
Hezčí grafy
pip install gpy

import GPy

rbf = GPy.kern.RBF(input_dim=1, variance=1.0, lengthscale=1.0)
gpr = GPy.models.GPRegression(X_train, Y_train, rbf)

# Zafixovat šum
gpr.Gaussian_noise.variance = noise**2
gpr.Gaussian_noise.variance.fix()

# Optimalizovat parametry
gpr.optimize()

# Výsledky
l = gpr.rbf.lengthscale.values[0]
sigma = np.sqrt(gpr.rbf.variance.values[0])

# Zobraz parametry (pandas)
display(gpr)

Model: GP regression
Objective: 3.8047835819738745
Number of Parameters: 3
Number of Optimization Parameters: 2
Updates: True

GP_regression.	value	constraints	priors
rbf.variance	0.5900032552941976	+ve
rbf.lengthscale	1.350129522839673	+ve
Gaussian_noise.variance	0.04000000000000001	+ve fixed

Knihovna GPy

gpr.plot()
plt.show()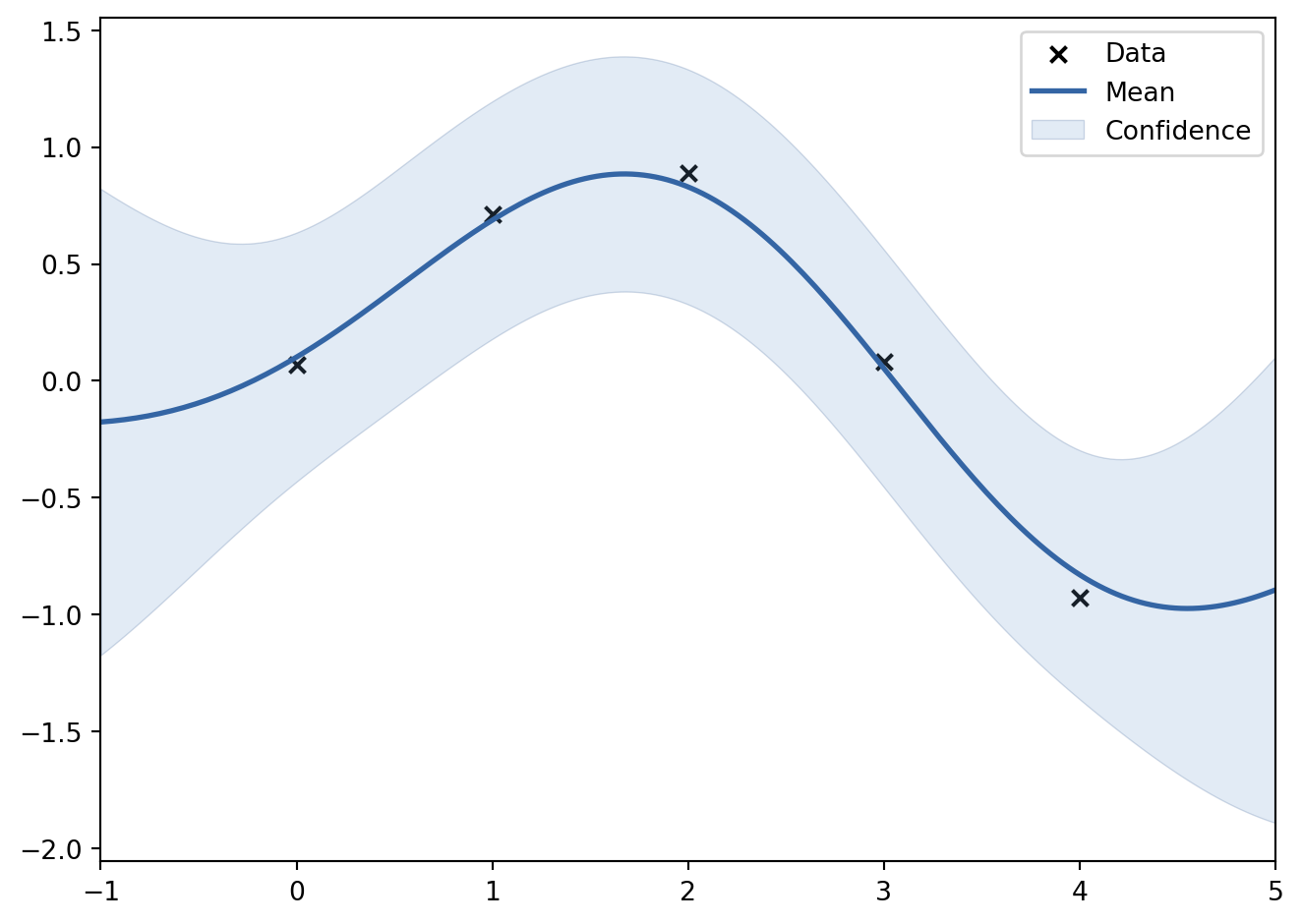

Bayesovská optimalizace

Co optimalizovat?

Funkce typu “black-box”

neznáme jaká funkce to je
nevíme její derivace
měření v bodě –> zašuměná odpověď

Co když měření trvá dlouho?

najít minimum za pomocí nejmenšího počtu měření

–> Bayesovská optimalizace! Potřebujeme:

Náhradní (Surrogate) model (GP!!)
Akviziční funkce - vymyslí na základě modelu, kde dále měřit

Akviziční funkce

hledá kompromis mezi
- průzkumem (exploration) - měřit tam, kde nic nevíme
- vytěžováním (exploitation) - měřit tom, kde se odhaduje minimum/maximum
používané funkce:
- “maximum probability of improvement” (MPI)
- “upper confidence bound” (UCB)
- “expected improvement” (EI)

\[ \mathrm{EI}(\mathbf{x}) = \mathbb{E}\max(f(\mathbf{x}) - \mathbf{y}^+, 0) \]

kde $\mathbf{y}$ je zatím nejlepší hodnota, $f(\mathbf{x})$ je náš gp model a $\mathbb{E}$ značí očekávání.

Scikit-optimize

import numpy as np
from sklearn.base import clone
from skopt import gp_minimize
from skopt.learning import GaussianProcessRegressor
from skopt.learning.gaussian_process.kernels import ConstantKernel, Matern
from helper import plot_approximation, plot_acquisition

bounds = np.array([[-1.0, 2.0]])
noise = 0.2

def f(X, noise=noise):
    return -np.sin(3*X) - X**2 + 0.7*X + noise * np.random.randn(*X.shape)

X_init = np.array([[-0.9], [1.1]])
Y_init = f(X_init)
# pro plotování:
X = np.arange(bounds[:, 0], bounds[:, 1], 0.01).reshape(-1, 1)
Y = f(X,0)

# Definice jádra
m52 = ConstantKernel(1.0) * Matern(length_scale=1.0, nu=2.5)
gpr = GaussianProcessRegressor(kernel=m52, alpha=noise**2)

r = gp_minimize(lambda x: -f(np.array(x))[0], 
                bounds.tolist(),
                base_estimator=gpr,
                acq_func='EI',      # expected improvement
                xi=0.01,            # exploitation-exploration trade-off
                n_calls=10,         # number of iterations
                n_random_starts=0,  # initial samples are provided
                x0=X_init.tolist(), # initial samples
                y0=-Y_init.ravel())

# Fit GP model to samples for plotting results
gpr.fit(r.x_iters, -r.func_vals)

# Plot the fitted model and the noisy samples
plot_approximation(gpr, X, Y, r.x_iters, -r.func_vals, show_legend=True)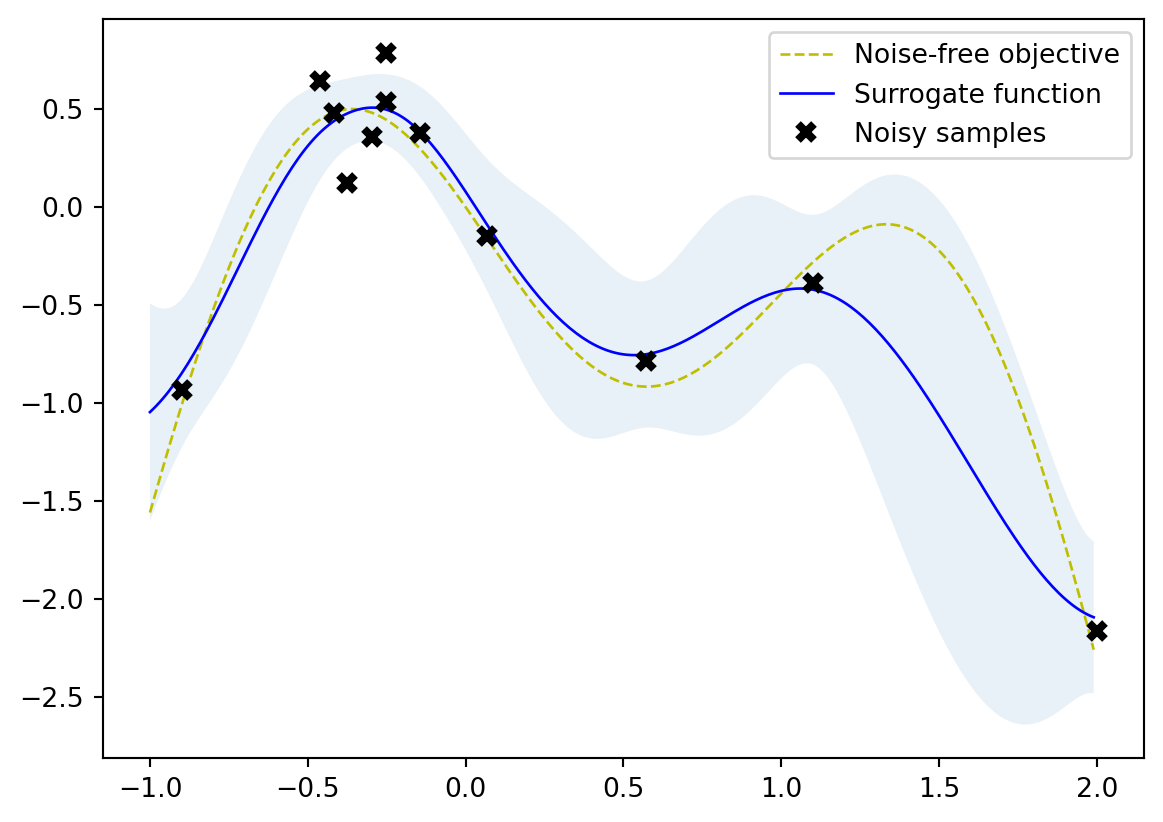

GPyOpt

import GPy
import GPyOpt

from GPyOpt.methods import BayesianOptimization

kernel = GPy.kern.Matern52(input_dim=1, variance=1.0, lengthscale=1.0)
bds = [{'name': 'X', 'type': 'continuous', 'domain': bounds.ravel()}]

optimizer = BayesianOptimization(f=f, 
                                 domain=bds,
                                 model_type='GP',
                                 kernel=kernel,
                                 acquisition_type ='EI',
                                 acquisition_jitter = 0.01,
                                 X=X_init,
                                 Y=-Y_init,
                                 noise_var = noise**2,
                                 exact_feval=False,
                                 normalize_Y=False,
                                 maximize=True)

optimizer.run_optimization(max_iter=10)
optimizer.plot_acquisition()

Other Formats

Připojte se

Statistika v kostce

Obecné pojmy - pravděpodobnostní model

Obecné pojmy

Gaussovské procesy

Gaussovský proces

Příklad jádra (kovarianční fce): RBF

Prior (nevíme nic)

Posterior

Zadáme data (bez šumu)

Zadáme data (se šumem)

Vliv parametrů

Optimální parametry

Více rozměrů

Jsou na to knihovny

Knihovna GPy

Knihovna GPy

Bayesovská optimalizace

Co optimalizovat?

Akviziční funkce

Scikit-optimize

GPyOpt